こんにちは、本年もどうぞよろしくお願い致します。

年始から松本城を見て来ました栗崎です。

(この前日が雪だったためお城の屋根瓦部分が溶けきっていない雪で薄らと白くなっています)

今年は暖冬傾向と言われていましたが年始はなかなか寒かったですね。

それを取り返すように今週は暖かそうです。

花粉よまだ飛ばないで

今年は午年、飛翔に駆け上るウマの年でございます。

ウマのように目標に向かって駆けていけるよう邁進してまいります。

 

さて、2026年。

新年一発目からマニアックなタイトルで失礼します。

とりあえず3桁4桁の数字を見るとやりたくなりますね、素因数分解。

※素因数分解とは、整数を素数の掛け算だけに分解していくことです

たとえば18という数字は、2×3×3に分解できます。

100という数字は2×2×5×5に分解できます。

2026年はなんと！

2×1013 でおしまいです。

あ、あまり分解できなかった。

1013って素数なんですね。

 

ちなみに来年2027も素数です、分解できません。

逆に去年の2025年はすごいです！

2025は3×3×3×3×5×5 に分解できます。

(なんと45の平方数というレア年でした)

 

さて、なんでこんなに素因数分解したがるのか。

それは算数でも数学でも

素因数分解が素早くできると計算が楽できるからです。

 

2023年の灘中学の入試問題にこんなものがありました。

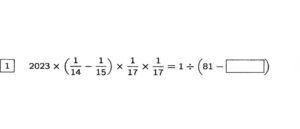
大問1と記載あるように、

最初の計算問題なのでものの数分で解かなくてはなりません。

2023、、、パッと見て5の倍数でも3の倍数でもないですね。

であればそのあとの17や14の数字が怪しい、

奇数なので7で割れそう。

とりあえず分解していきましょう。

2023は7×289

17で割ろうとしてるからいけそう

289を17で割ると、17！

2023を素因数分解すると7×17×17！

これが分かれば計算は簡単！

左側の計算が簡略化できて1/30という答えが出て来ますので

それに合う答えになるように右側の四角の数字が埋まります。

 

この素因数分解、高校入試や大学入試でも数学問題でフル活用する技術です。

 

3の倍数は各桁の数字を足すと3で割れる

9の倍数は各桁の数字を足すと9で割れる

5の倍数は1の位が0か5、

などを抑えながら

大きい数字を、小さい数字の掛け合わせに分解できるスキルがあると

数学の計算問題に役立ちます。

(二次方程式の因数分解でもここが早いと解く速度がグッと上がります)

 

ぜひ新年を迎えたら、あるいは3桁4桁の数字を見かけたら、素因数分解してみましょう。

(入試って西暦年をかけた問題を出すの好きですよね)

ちなみに2027と2029は素数ですので分解できないです。

わずか1年置きで素数年がくるレア年でもありますが。

 

以上、素数年生まれの栗崎でした。