こんにちは、今朝からソワソワしている栗崎です。

今日は教室のクリスマス会🎄

コロナ禍以降初（3年ぶり）の集合形式のクリスマス会を予定しています！

ビンゴゲームに⚪︎×クイズ、じゃんけん大会！

申し込みしてくれたみんな、教室でお待ちしてます。

また、今日は残念ながら予定があってこられない生徒さんも

来週以降のレッスンでクリスマスのお菓子＆

下記質問表を持ってきてくれたら妖怪カードをお渡しするのでお楽しみに☺︎

そして今年もブログでこっそりと、

クリスマスなので算数クイズ！

生徒の栗崎さんがクリスマス会に参加すべく

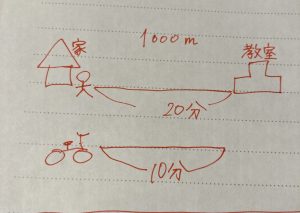
朝9時30分に家を出ました。

歩いて20分で教室に着く予定です。

9時35分、娘の忘れ物に気づいた母が自転車で追いかけます。

自転車だと10分で教室に着きます。

さて自転車に乗った母が娘に追いつくのは何時何分でしょう？

この問題の肝は、時間しか聞かれていないという点。

家から教室までの距離も、歩きと自転車の速度も不明。

ちなみに距離と速度と時間の関係は

距離＝速度×時間で表せます。

今回時間が問われてるので上の式を置き換えると

時間＝距離÷速度になります。

この３つのうち２つが不明。

しかし問われてるのは時間のみ。

解き方はいくつかありますが

その一つとして、

計算しやすい距離を適当に置いてしまう方法があります。

家から教室までの距離を1,000mとします。

歩きの速度は

1,000m÷20分＝50m/分

自転車の速度は

1,000m÷10分＝100m/分

母がスタートする時点で5分経過していますので

娘はすでに

50m/分×5分＝250m

進んでいます。

さて、ここで注意！

娘が250m進んでるから、母が追いつくのは

250m÷100m/分＝2.5分！　2分半で追いつく！

と計算してしまうのはまさに早計です！

母が自転車で追いかける間も、娘は歩きでどんどん進んでいきます。

二人の速度の差は

100m/分−50m/分＝50m/分

1分ごとに50m追いつくということになります。

二人の距離が250m。

この距離が埋まるのは

250m÷50m/分＝5分。

なので追いつくのは母がスタートしてから5分後。

母のスタートは9時35分なので9時40分に娘に追いつきます。

この追いかける問題は旅人算といいます。

今回の問題では距離を適当に置く、というのがポイントになりますが

もし二人の進む時間が7分、3分といった数字が出てきた場合

距離を7や3の最小公倍数に置き換えましょう。

割り切れない数字でやると分数が出てきて厄介なので、計算が楽な数字を作るのがおすすめです。

（ちなみに自転車の速度ゆったりだな、という感覚が生じた方、素晴らしいです。

計算が楽になるよう適当な数値を入れているので、平均より遅いです笑）

みんなは忘れ物しないできてね〜！

栗崎